Linear Regression with multiple variables
It is common to consider more than one features when making a prediction. For example when predicting the price of a house:
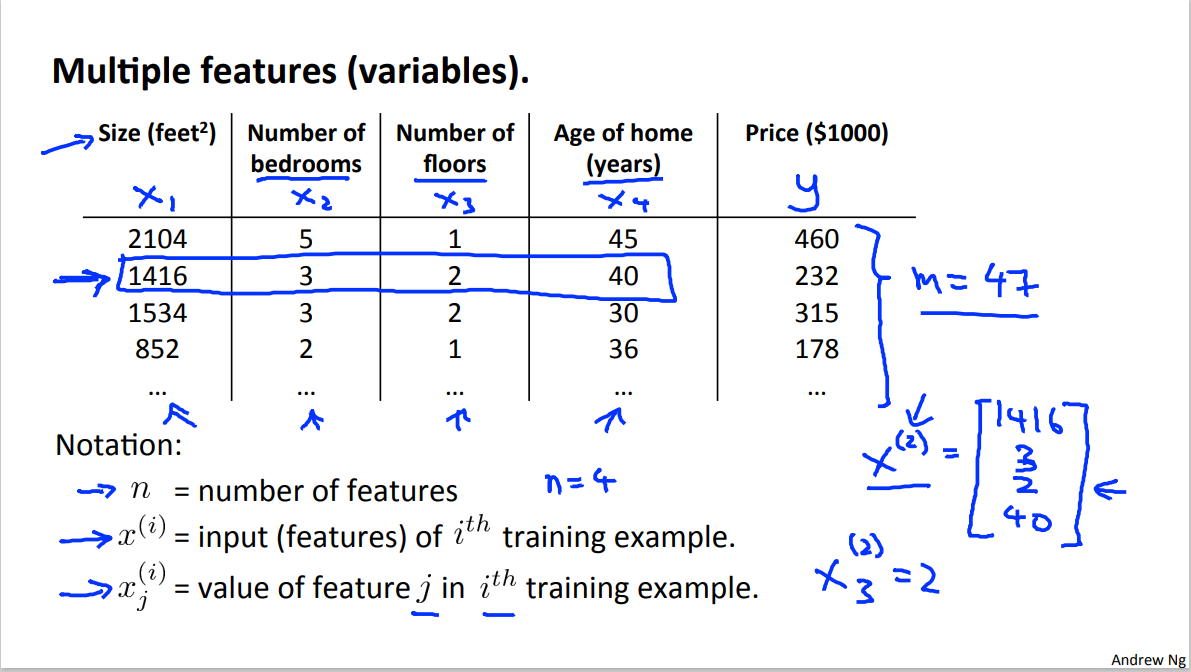
Hence more generally hypothesis function can be written as: $$ h_\theta(x)=\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3+…+\theta_n x_n $$ $$ =\theta^Tx $$ Where $\theta$ is $$ \begin{bmatrix}\theta_0\ \theta_1\ \vdots \ \theta_n \end{bmatrix} $$ Also more generally, gradient descent algorithm can be written as: $$ \theta_j := \theta_j - \alpha\frac{1}{m}\sum^m_{i=1}[h_\theta(x^{(i)}-y^{(i)})]x_j^{(i)} $$ $$ (simutaneously\ update\ \theta_j\ for\ j=0,\cdots,n) $$
However, it also comes with some problem:
The choice of learning rate
may affect the speed of converge, or even can not converge.
The scale of number of examples and features may affect the speed of algorithm
The common linear regression is a straight line that may can not fit the data well
Feature Scaling
When there is a big magnitude difference between different features in a cost function, it could take a lot of time to iterate to find the converging point, for example:
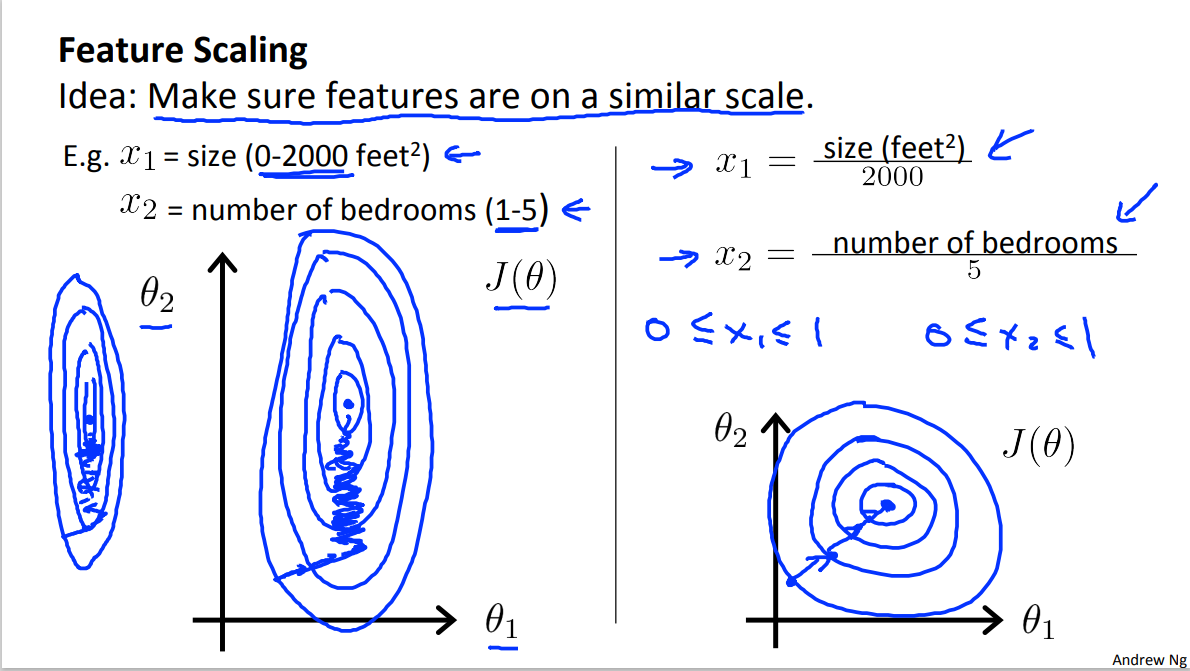
By using the feature scaling, we aim to scale these different features to a similar range (roughly between -1 to 1). The common method of featuring scaling is mean normalization:
Mean normalization
$$ X_{norm} = \frac{x_n - \mu_n}{s_n} $$
Where
- $\mu_n$ is the average value
- $S_n$ is the range of the feature (maximum - minimum)
Polynomial Regression
As just mentioned, the common linear regression is a straight line that may can not fit the data well, some times we need curve to fit the data.
For example, we may want a quadradic function $h_\theta(x)=\theta_0 +\theta_1 x_1 + \theta_2 x^2_2$. Assuming: x_2 = x_2^2, to covert the quadratic function to a linear model which we are more familiar with
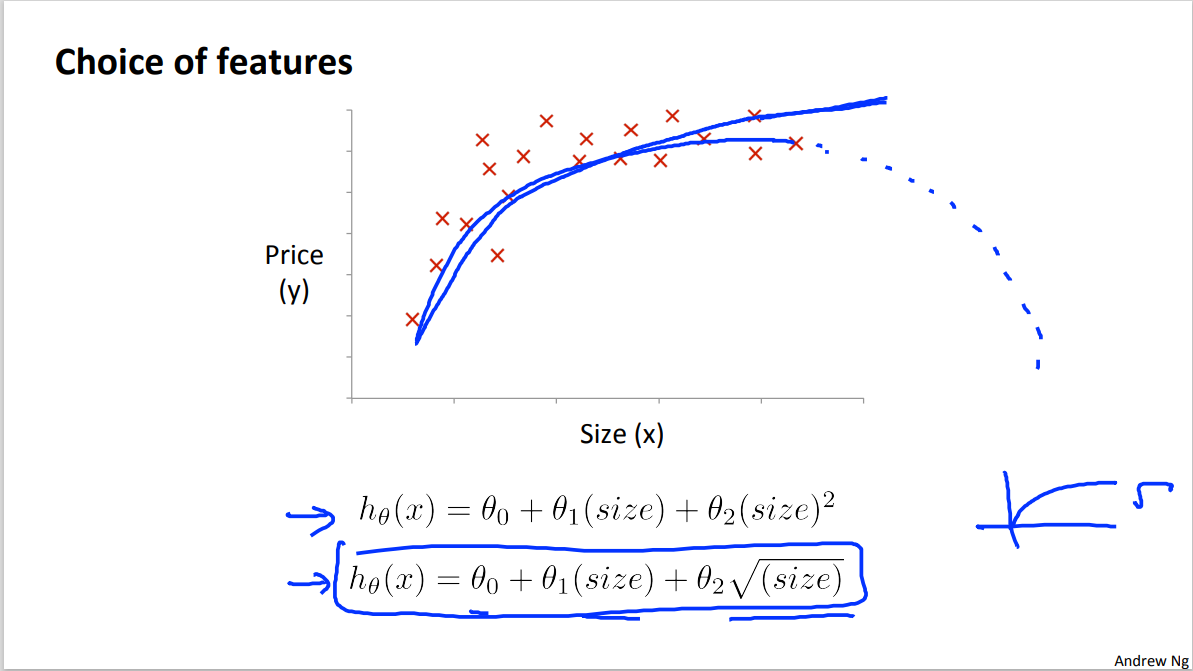
Note: It is obvious that we need to scale the feature in polynomial regression since the features are more different from each other .