What is Option Trading ?

  • A security giving the right to buy or sell an asset, subject to certain conditions, with a specified period of time.

  • Strike Price θ‘Œζƒδ»·οΌ› Premium ζœŸζƒδ»·οΌ›

  • European Option: Exercisable only on the expiration date. American Option: Can be exercised at any time before the expiration date.

    image-20250222143349581

  • When the stock price is much greater than theexercise price, the option is almost sure to be exercised. The current value ofthe option will thus be approximately equal to the price of the stock minusthe price of a pure discount bond that matures on the same date as theoption, with a face value equal to the striking price of the option.

    • The current value of option = current stock price - strike Price value as of today
    • Option Value = ReLU(Asset Price - Strike Price * Discounted Factor)
    • strike Price value as of today can be represented by a zero-coupon bond, with a face value same as strike price and same maturity date.

Black Schole Formula:

  • A standarlized way to price the option.

  • The model is based on Geometric Brownian Motion, a stochastic differential equation used to represent a random process, the theory is derived from the Delta Hedging hypothesis.

  • For a Eupropean style call Option, the price/premium of the option is described as C=N(d1)Stβˆ’N(d2)Keβˆ’rt C =N(d_1)S_t - N(d_2)Ke^{-rt} Where: d1=InstK+(r+Οƒ22)tΟƒt d_1 = \frac{In\frac{s_t}{K}+(r+\frac{\sigma^2}{2})t}{\sigma\sqrt{t}}

    d2=d1βˆ’Οƒt d_2 = d_1 -\sigma\sqrt{t}

  • C: option preimum

  • S_t: Spot price of underlying asset

  • K: Strike Price

  • r: risk free interest rate

  • t: time to matuirty

  • Sigma: volatility

Moneyness, ITM, ATM and OTM:

Moneyness is used to describe the intrinsic value, regardless of absolute strike price and underlying price:

  • In-the-Money (ITM):
    • Call: S>KS>K (e.g., S=100S=100, K=90K=90 β†’ intrinsic value = $10).
    • Put: S<KS<K (e.g., S=100S=100, K=110K=110 β†’ intrinsic value = $10).
  • At-the-Money (ATM): Sβ‰ˆKSβ‰ˆK (intrinsic value β‰ˆ $0).
  • Out-of-the-Money (OTM):
    • Call: S<K; Put: S>K, (intrinsic value = $0).

Quantifying Moneyness

  • Simple Ratio:

    • Call: S/KS/K; Put: K/SK/S. Values >1 indicate ITM for calls (OTM for puts).

  • Log-Normalized Measure:

    Moneyness=ln⁑(S/K)ΟƒTMoneyness=Οƒ**Tln(S/K)

    Standardizes price deviation for volatility modeling.

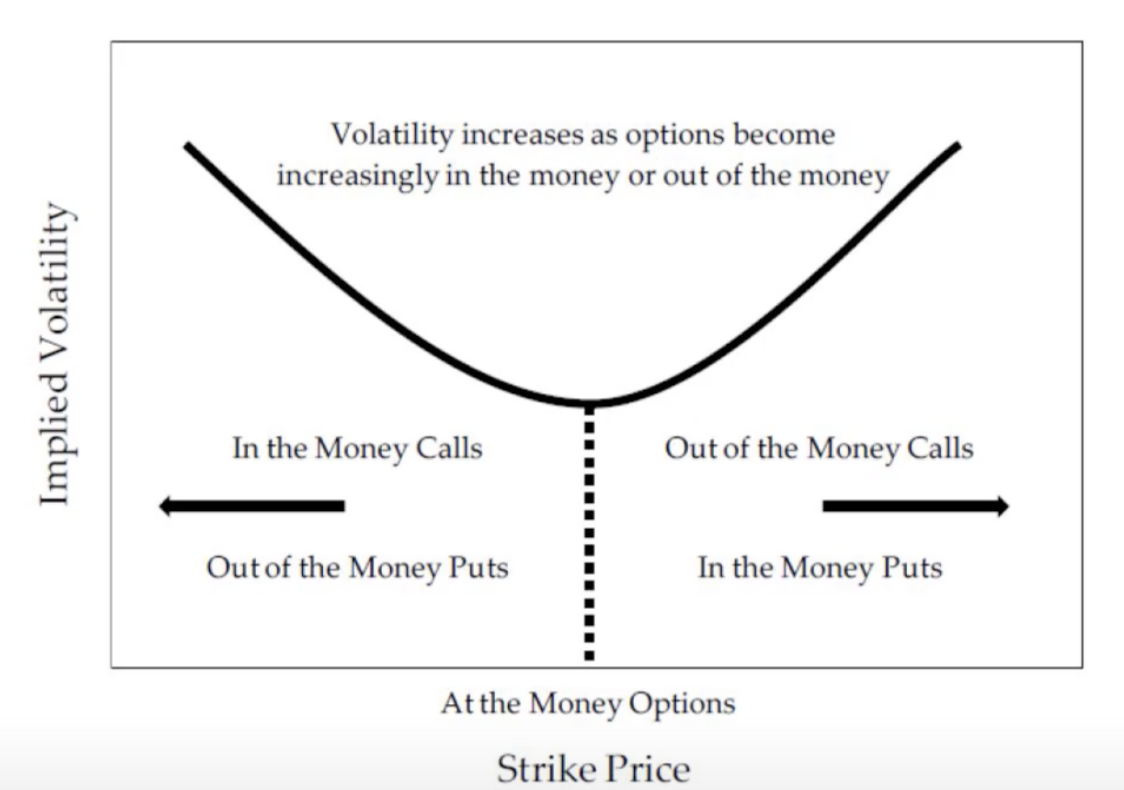
Volatility and Volatility Surface:

In theory, BS Model assumes volatility as a constant.i.e. ΟƒβˆˆN\sigma \in N, for example, we have two call options on the same underlying future contract, but with different strike. These two options should have the same volatility. HOWEVER, Οƒ\sigma changes with strike and time in the real market, when pricing the option, we usually derive the volatility from the historical market data, this is called implied volatility, i.e. Οƒ=f(K,T)\sigma = f(K,T)

The different patterns of vol (volatility) surface can leads two common style of curve:

Smile Surve (due to fat tail distributions):

image-20250222152754781