Monte Carlo Tree Search Summary

Vanilla MCTS

http://www.incompleteideas.net/609%20dropbox/other%20readings%20and%20resources/MCTS-survey.pdf

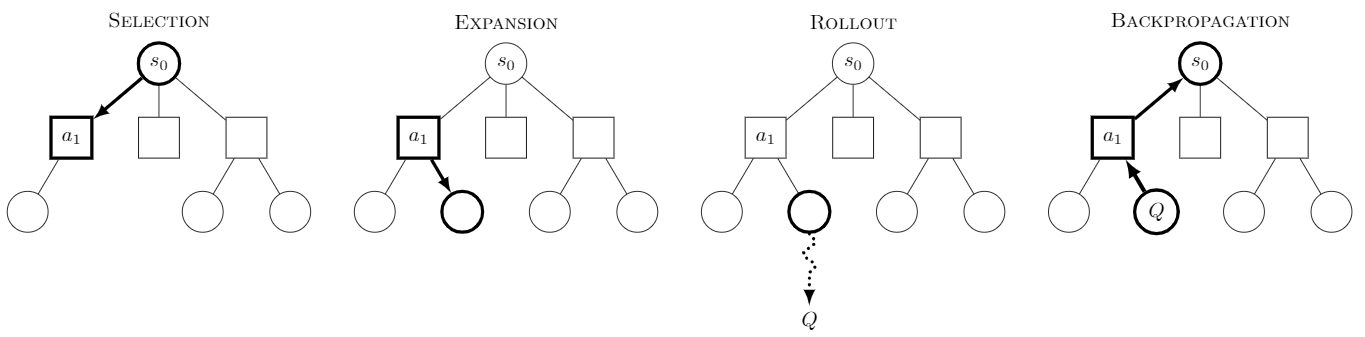
Searching Process

Starting from $S_0$ :

• Selection:

  • Two statistic information:

    1. Visit count $N(V)$
    2. Win count $Q(V)$

  • Selection the possible action by Upper Confidence Bound for Tree (UCT): $$ UTC(v’) = \frac{Q(V’)}{N(V’)}+c\sqrt{\frac{InN(V)}{N(V’)}} $$

​ Until the most urgent expandable node is reached. A Expandable Node is the node that has one or mode child node haven’t been explored.

• Expansion:
  • Adding the child node to the current node
• Rollout:
  • Start from the current leaf node, taking a random sequence of actions to play the game until reaching to the end.
• Back-propogation:
  • Backup the simulation result through the selected nodes to update their statistics

Note:

• The UCT score could be treated as two components: The exploitation part and the exploration part
  • In exploitation part: $Q(v)$ is the rewards of all play out that pass the node $v$ , $N(v)$ is the visit count.

MCTS in Alpha Go

https://www.nature.com/articles/nature16961

Networks

2 policy networks

• $P_\sigma (a|s)$ Supervised Learning policy network

  • Input: Simple representation of the board state
  • Output: Probability distribution over all legal movement
  • Goal: Maximize the likelihood of the huaman move a selected in State s

• $P_\pi (a|s)$ Reinforcemet Learning policy network

  • Identical Structure as $P_\sigma$
  • Goal: Maximize the expected outcome

1 value network

• $V_\theta(s) $ RL value network
  • Input: State preresentation
  • Output: outcome from the current position

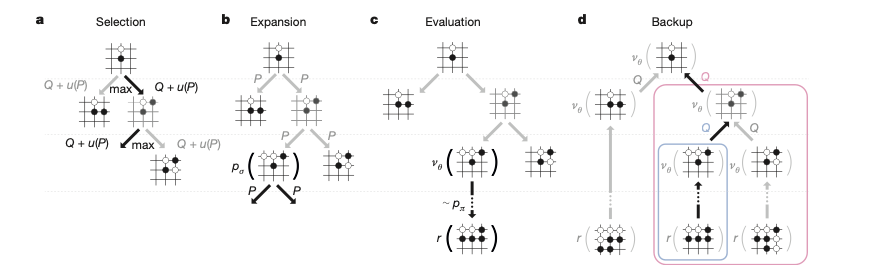
Searching Process

• Selection:

  • Three Statistic Info on each node (s, a):

    1. Visit count

    2. Prior Probability, predicted by $p_\sigma(a|s)$

    3. Action Value $Q(s,a)$: Average evaluation of all simulation passing through that each

  • Traversing the tree by selecting the edge with max mark, where mark is $$ Q + u(P) $$

• Expansion:

  • The expanded node will be processed by $P_\sigma $, generating the prior probability of each poential actions.

• Evaluation:

  • The Leaf node will be evaluated by two ways $$ V(S_L) = (1-\lambda)v_\theta(s_L) + \lambda z_L $$
  1. Evaluating the node by $V_\theta$
  2. Evaluating the node by continuing playing the game from the state $$S_L$$ (Same as before), while using $$P_\pi$$ to sample actions. At the end of the game, using an evaluation function.

• Backup:

  • Update the visit count and mean evaluation recursively.

MCTS in Alpha Go Zero

https://discovery.ucl.ac.uk/id/eprint/10045895/1/agz_unformatted_nature.pdf

Network

• One network $f(\theta)$ to replace the value evaluate net and policy net in the previous one
• Input:
  • A sequence of representation of board position: raw board representation s of the position and its history
• Ouput:
  1. $Pr(a|s)$ Probability of each action, Vector
  2. $V(s,a)$ Evalution of current $(s,a)$, Scalar

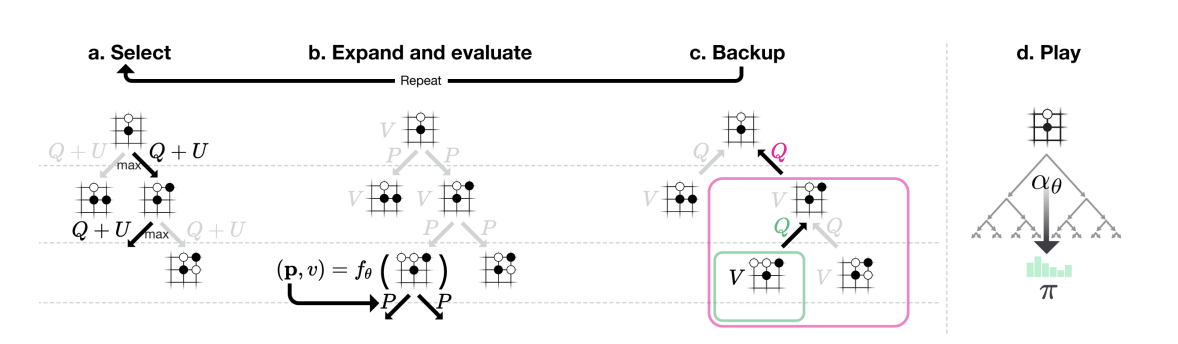
Searching Process

• Selection:

  • Same as before, where $$ U(s,a) \propto \frac{P(s,a)}{1+N(s,a)} $$

• Expansion and Evaluation:

  • Instead of continue exceuting the game, the evaluation of the expanded node is directly predicted by $f(\theta)$ , same for the prior probability

• Evaluation:

  • Action-values Q are updated to track the mean of all evaluations V in the subtree below that action

MCTS in MuZero

https://www.nature.com/articles/s41586-020-03051-4

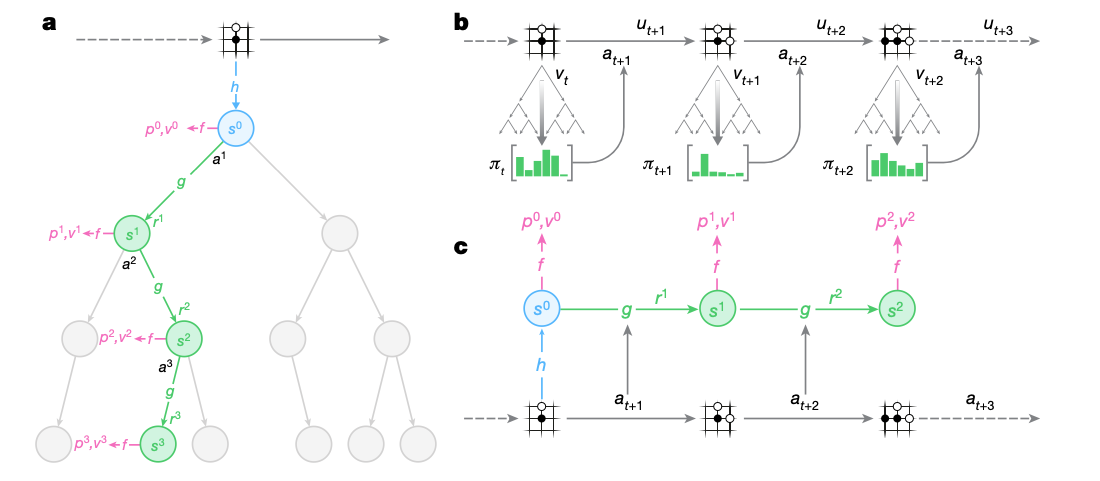
• Without the simulator:
  • No state transitions
  • No Terminate states
  • No actions restriction

Networks

All parameters are trained jointly

• Representation function h:

  • Encoding the history over board states into the internal state $s$ $$ s = h_\theta(o_1,\cdots,o_t) $$

• Perdiction function f :

  • same architecture as AlphaZero

  $$ p_k,v_k = f_{\theta}(s_k) $$

• Dynamics function g:

  • Mirror the structure of MDP, a recurrent process $$ r_k,s_k=g_{\theta}(s_{k-1},a_k) $$

Searching process

• Observation Encoding by representation function $h(s)$

• Selection:

  • Each node contains 5 statistic info:

    • Visit count
    • Policy
    • Mean value
    • Reward
    • State transistion (Internal root state)

  • According to probabilistic upper confidence tree bound

• Expansion:

  • Create the new node
  • Reward and state are from the dynamic function $r’,s’=g_{\theta}(s,a’)$
  • Policy and Value are from predcition function $p’,v’=f_{\theta}(s’)$
  • Mean value and visit cound are initialized as 0

• Backup

MCTS in Sampled Alpha Zero

http://proceedings.mlr.press/v139/hubert21a/hubert21a.pdf