Common Terminologies in Graph Thoery
Define an undirected graph with the natrual order as $G = (V,E,\sigma)$ where $V$ is the set of the vertices, $E$ is the set of edges and $\sigma$ is the natrual ordering.
Chordal graph
- A chordal is a path of undirected graph between two non-conescutive vertices. (“shortcut”" between two vertices")
- A chordal graph referes to every cycle of length four or greater of a simple graph has a chord. (triangulated graph)
Chordal Completion
- The triangualtion result of an undirected graph, it is a chordal graph
Filled Graph
- An undirected graph $G$ is filled graph if any two higher order neighbours of any vertex in $G$ induce an edge $$ w,z\in adj^+(G) \rightarrow {w,z}\in E $$
Elimination order
- An elimination ordering $\sigma$ is a numbering of the vertices of $G$ from 1 to n.
- The fill-in $F_{\sigma}$, caused by the ordering $\sigma$ is the set of edges defined as: $F={{w,v}|w\neq v, {w,v}\neq E}$
Perfect Elimination Order
- $\sigma$ is perfect if $F_\sigma=\phi$
- $\sigma ^$ is the perfect elimination order if $G=(V,E,\sigma ^)$ is a filled graph. (Eliminate by this order wouldn’t create any new chordal)
- A graph is chordal if and only if it has a perfect elimination order
Complete Graph
- A graph is complete if all vertices are pair-wise advanct
Clique
- A clique is a subgraph of $G$ that is complete
Simplicial Vertex
- A simplicial vertex is one whose neighbours forms a clique
Vertex seperator
- If $S$ is a subset of the vertices: $S\in V$, $G(V\backslash S)$ is the subgraph of $G$ induced by $S$; if $G(V\backslash S)$ is disconnected, $S$ is a separator.
Clique Tree
- A clique tree of a graph G = (V,E) is a tree which has the cliques of G as its vertices.
Block (Read more from this paper)
- the set of minimal seperator $S\in\triangle(G)$
- the set of connected componets w.r.t $S$: $\mathcal{C}_G(S)$
- The component is a full component with S if every vertex of S is adjacent to some vertex of C.
- If $C\in\mathcal{C}(S)$, $(S,C)=S\cup C$ a block associated with S
- The block is called full if C is a full component associated with S
The Difference between Minimal and Minimum
Since the problem of computing minimum triangulations is NP-hard, the related polynomially solvable problem of computing minimal triangulations became interesting, and the first algorithms for it appeared in 1976
It should be emphasized here that the word “optimal” should not be mistaken to mean “optimum” as in some engineering literature. In terms of a set, “optimal” refers to a set property, whereas “optimum” refers to the size of the set.
—Minimal Triangulation of a Graph and Optimal Pivoting Order in a Sparse Matrix (Ohtsuki, etc, 1976)
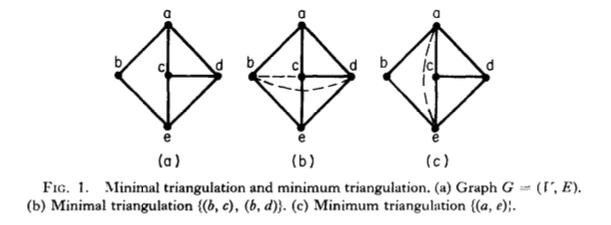
Block realisation
Potential Maximal Clique: a potential maximal clique if there is a minimal triangulation H of G such that Ω is a maximal clique of H.